If you’re like me, you think videogame music is pretty neat. Also, if you’re like me, you’ve had the theme from the original Super Mario Brothers playing in your head incessantly for the last like three years and OH GOD WHEN WILL IT STOP.

Super Mario Bros Ground Theme by Koji Kondo (1985)

 

The term “videogame music,” though, has at least two different meanings. One is simply any music originally produced for a videogame. The second, which is probably the more common one in use these days, is the genre of music known as “chiptunes.” These are the characteristic beepity–boopity music produced by the 8-bit (or, if you were lucky, 16-bit) chipsets in use in games during the earlier part of the console era (up to Super Nintendo / Sega Genesis).

While it was the technological limitations of the time that forced creators to strip down the sorts of sounds they used for games – just as the same limitations required them to use pixel art for the visuals – the best composers still managed to produce such charming and iconic pieces that they’ve stuck in our imaginations as strongly as any of those 80s earworms that began incorporating synthesizers at around the same time.

Megaman 3 Intro by Yasuaki Fujita a.k.a Bun Bun (1990)

While electronic sounds were an expansion of the palette for rock bands then, they were the palette for videogame music. Now that technological progress has caused those limitations to pretty much disappear, we see videogame composers creating entire symphonies to accompany the nearly-photorealistic visuals of contemporary games. Witness the development of the soundtracks from the long-running Final Fantasy series, wherein the work Nobuo Uematsu’s work has progressed from simple chiptunes through to the epic scope of Sephiroth’s theme from FF7 (on the Sony PlayStation 1997), “One-Winged Angel” – which the composer described as intended to be a fusion of Stravinsky and Jimi Hendrix – and beyond.

 

“Something something something something SEPHIROTH!!!”

 

As actual videogames moved away from the requirements of music that sounded as if a computer produced it, we began to see the proliferation of musicians who were using outdated technology to create original music that deliberately sounded as if it had come out of a videogame from 1989, even though the music was not at all associated with any actual videogame besides the sonic nostalgia. Chiptunes had started to become a genuine genre, rather than a technological compromise.

 

Savestates – “Searching for Resolution” (2012)

 

But rather than dismiss this development as pure irony, as just making fun of the primitive state of videogame music that existed when these bands and their fans were young and impressionable, I think it’s more accurate to look at it in another way: as a musical parallel of the sort of experimenting with limitations that we saw in visual art in the Modern Art of the early-to-mid-Twentieth Century, in particular the Di Stijl and Pop Art movements.

Piet Mondrian was one of the originators of De Stijl in the 1920s. Influenced by Picasso and Cubism, Mondrian quickly evolved from representational painting into the totally abstract; his characteristic style became the grid-like depictions of squares, rectangles, and lines, in black and white, and bright primary colours. Mondrian felt that this was the most faithful way to depict the spiritual purity of the forces that underlie the world’s physical nature.

Pretty, right? By deliberately restricting the colours and shapes that he used in his work, Mondrian was able to create a style epitomized by its variations on a theme. While the trend in painting was moving beyond the boundaries of representation that, for many artists, freed them to depict the world in a more subjective way than had been generally permissible in the past, Mondrian found freedom in limitation; much as how the rules of meter and rhyme in formal poetry set out guidelines within which one had to work harder to express things in the ways that were allowed, Mondrian’s self-constraints forced him to exert a much stronger degree of creativity than he would have required if he could just have done anything. That also makes the small changes, subtle distinctions, and incremental evolution of the style over time, to feel much more surprising and significant.

The similarities between Mondrian and chiptunes, though, are analogous in more ways that just this. The actual visual forms have some striking correspondences, too. Mondrian was interested in using geometric shapes to illustrate what he thought of as transcendental truths. But if we look at 8-bit music – I mean literally look at it – it turns out that those beepity–boopity noises are the sonic manifestation of geometric figures as well.

Most of the sounds that we hear are produced naturally – that is, not electronically. Voices, musical instruments, trees falling in the woods, all produce sounds that can be expressed visually as a round wave, or sine wave. You could call these “analogue” sounds. Mathematically, sine waves are the sum of a square wave and a triangle wave, which are “digital” sounds – digital because they are the expression of vibrations that are integral multiples of their lowest given frequency, rather than increasing or decreasing more incrementally the way natural sounds do.[1]

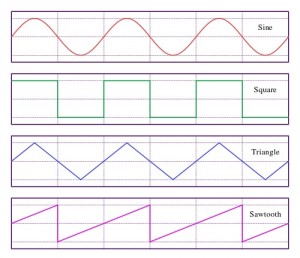
Chiptunes, though, since they are produced digitally by definition, don’t have sine waves at all. They’re purely square waves and triangle waves. They’re generated mathematically, rather than, as it were, organically. And that’s what gives them that distinctively artificial character: the actual shape of the sound is geometrically distinct from anything that could be generated more “naturally.”

 

Zelda Chiptune Visualization

 

So both Mondrian and chiptune composers used geometric shapes and “digitalness” to evoke a new kind of reaction to art; when previously much of art was representational, both chiptunes and De Stijl subverted attempt to appear “organic” and chose instead to represent a more idealized version of reality (“ideal” in the Platonic sense). In both cases, the end result is a synthetic-seeming artifact that nevertheless is a more authentic expression of what underlies reality on a level we don’t normally appreciate – for Mondrian, this was the spiritual perfection of straight lines and primary colours; for chiptunes, it was the squares and triangles that combine in nature into the round sounds we hear every day.

But of course, the earliest chiptunes weren’t doing this on purpose. Digital music wasn’t an artistic choice back then, but a technological necessity – a compromise with externally imposed limitations. The music you’ll hear in the most advanced videogames today isn’t really chiptunes at all. You can put a full orchestra and chorus in a game now, if you want to. And even if the sounds are synthetically generated, they don’t have to sound as if they are. This is the point at which chiptunes became a genre in and of itself, an artistic decision. And this is where the parallel with pop art kicks in – most accurately, with the work of Roy Lichtenstein.

In the early-to-mid 1960s, Lichtenstein became interested in comic books. In the 1950s and 60s, most comic books were printed using a process called “Ben-Day Dots” (which, to me, sounds like something that could have got you in trouble with the Comics Code Authority, but whatever), wherein patterns of small yellow, black, cyan, and magenta dots were used to simulate more complex (and more expensive) colours. So, for instance, instead of using beige-coloured ink for Batman’s skin tone, you could use magenta-coloured dots and space them out so that when printed at a certain size and looked at from a certain distance, it would look pretty much like he was a regular Caucasian. This is also why sometimes, in those old comics, if they didn’t get the spacing quite right, Bruce Wayne looked as if he was suffering from really bad eczema.

 

Technology marches on, of course, so while you’ll practically never see Ben-Day dots in contemporary comic books – both because it’s much cheaper to print in colour these days, and also because we’re now willing to pay four bucks for one goddamn comic that’s still full of ads, when they never would have put up with that crap back in the day – Lichtenstein wanted to take what was a limitation of the printing process and turn it into a deliberate effect. By keeping the proportions of the image constant but painting it on a much larger canvas, the dots themselves became the most notable quality of the work. He emphasized the constructedness of the image rather than attempting to minimize it. And so he became famous for his deconstructions/reconstructions of what was at the time considered to be one of the lowest forms of art – if it was considered to be art at all. Its artificiality became the point of it, rather than a necessary evil or an unfortunate but unavoidable byproduct of the creative process.

 

The parallel with videogames is again apparent; while at first the limitations on games were technological whereas visual art was limited more by tradition, once it was possible for videogame composers to create any sounds they wanted to, creating chiptunes suddenly became a choice that carried extra significance precisely because of how it shrank the field of potential into something that made the artist’s decisions orders of magnitudes more meaningful.

And now we’ve managed to come full-circle, with stuff like the chiptune rock band Anamanaguchi providing music for the pixel-art throwback videogame adaptation of Bryan Lee O’Malley’s Scott Pilgrim graphic novel series, itself heavily influenced by the tropes and style of the old-school games the artist played in his formative years (most especially the 1989 NES classic River City Ransom). Everything about the Scott Pilgrim game is meant to evoke the early console era; as a pastiche of those sorts of games, its relentless authenticity lies in its adherence to the technologically-mandated limitations that made games at the time what they were.

The nostalgia that so many of us feel for those games – and for the music that went along with them – is not solely a yearning for a simpler, bygone time, when we were young and care-free. It’s also, in large part, recognizing and embracing that because so much was genuinely impossible for the creators of those games they were forced to be more creative than they otherwise might have been, to solve puzzles with an extremely minimal number of possible pieces; a lot like when the astronauts had to repair Apollo 13 by sticking chewing gum to a mailbox.

As a genre, then, chiptunes has a lot in common with some of the movements in visual art of the Twentieth Century. And as we can see, far from reducing our possibilities for expression, experimenting with limitations can ultimately end up making our creative toolbox all the more expansive.